项目中需要使用前缀树匹配,对此进行了简单的调研和整理。
概述
前缀树(trie),顾名思义,一般用来匹配和查找字符串的前缀。trie的键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。 trie实际上是一种DFA。输入字符串根据当前的输入的字符决定是否向下,以及去往哪个子节点。
实现分类
trie树实现:一般的链表指针方式,三数组实现,双数组实现,HAT,burst trie等。
-
链表指针方式
- 即每个节点对应一个字符,并有多个指针指向儿子,查找和插入从根节点按照指针的指向向下查询。这种方案,实现较为简单,但指针较多,较为浪费空间;树形结构,指针跳转,对cache不够友好,节点数目上去之后,效率不够高。
-
HAT以及Burst trie
- 是将trie树和其他数据结构,比如HashMap,结合起来,提高效率。但主要用于key/value查找,对于给定一个字符串匹配其前缀这种场景不适用。
-
三数组实现
- 利用三个数组(分别叫做base, next, check)来实现状态的转移,将前缀树压缩到三个数据里,能够较好的节省内存;数组的方式也能较好的利用缓存。
-
双数组实现
- 是在三数组的基础上,将base数组重用为next数组,节省了一个数组,并没有增加其他开销。与三数组相比,内存使用和效率进一步提升。
综上,双数组trie(Double Array trie,简称为DATrie)的实现有明显的优势,以下只讨论DATrie的细节。
DATrie算法
结构
-
数组表示trie树的状态转移,父节点跳转到子节点转化为父状态跳转到子状态
-
利用两个数组base, check表示状态的转移
- base数组的索引用来表示状态
- base数组的内容为状态跳转的基地址
- 输入字符为跳转的offset
- check与base大小相同,一一对应,用于保存父状态,以及解决冲突
-
对于状态S接收到字符c后转移到状态T $$ S\xrightarrow{c} T $$ 满足
1
2check[base[S] + c] = S
base[S] + c = T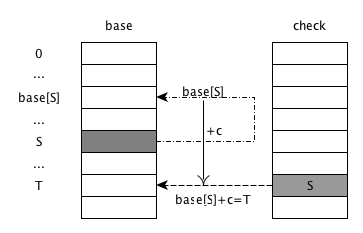
- base数组的索引为0,1,…, base[s], …, S, …, T,均表示trie树的状态
- 从S状态接收到c跳转到T, 则表示为base数组索引为S的内容base[S]为基地址,加上跳转偏移c,得到下一个T状态在base的索引T=base[S] + C
- check数组对应T的内容check[T]为跳转过来的父状态即S
查询
- 从base数组索引0开始,初始状态为S=base[0],其中偏移的基地址为base[S]
- 接受到c,则跳转到base数组索引T=base[S] + c,检查此时check数组的check[T] == S,为真跳转到3,否则匹配失败。
- 如果base[T] == LEAF_VALUE (这里LEAF_VALUE用来表示叶子节点的特殊值),则匹配完成;否则,令S = T, 跳转到2.
状态更新的伪码如下
1
2
3
4
5
6
7T := base[S] + c;
if check[T] = S then
next state := T
else
fail
endif
例子
- 假定输入两个前缀为'ab', 'ad',将字母a-z映射为数字1,2,3,…, 26.
- 这里用-1代表数组元素为空,-2代表叶子节点, -3代表根节点
- 状态如下
-
初始状态
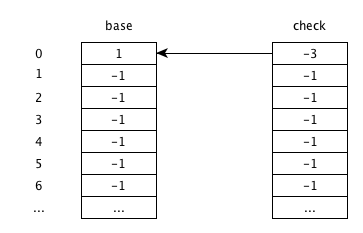
对于索引0,check[0]=-3代表根节点, base[0]表示偏移基地址为1,其他元素为-1表示为空
-
输入前缀ab
-
输入a
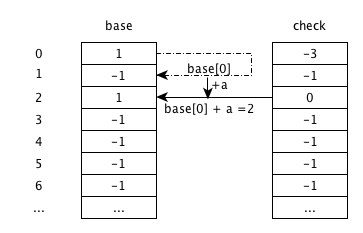
base[0]+a,由状态0跳转到状态2. check[2]为-1,说明为空,更新为父状态0;base[2]更新为跳转过来的base, 即base[0]的值1
-
输入b
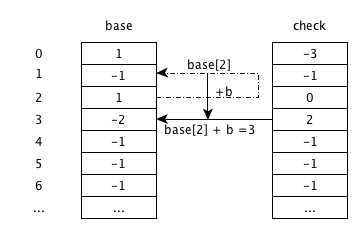
base[2]+b,由状态2跳转到状态3,check[3]为-1,说明为空,更新为父状态2;由于字符串结束,将base[3]更新为-2,代表叶节点。
-
-
输入前缀ad
-
输入a
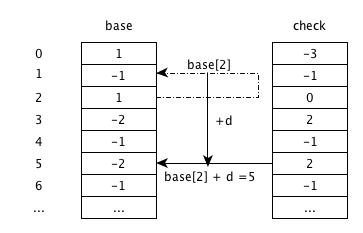
图中base和check的状态不会变化。 根据base[0]+a,从状态0跳转到2。 check[2]不为空,但check[2]的值0与其父状态S=0相等,则无需更新,进入状态2,等待输入下一个字符。这个过程相当于一个查询过程
-
输入d
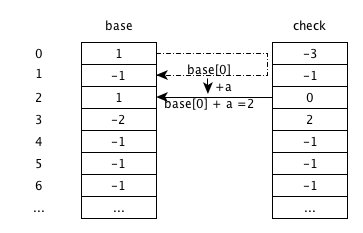
base[2]+d,由状态2跳转到状态5,check[5]为-1,说明为空,更新为父状态2;由于字符串结束,将base[5]更新为-2,代表叶节点。
-
-
解决冲突
DATrie不可避免会出现冲突
- 以上例子,假设接着输入字符串ca
-
输入c
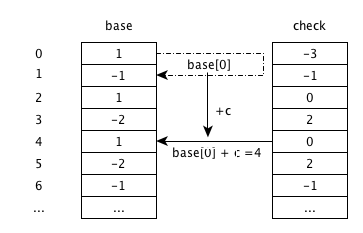
状态由0跳转到状态4,check[4]空闲,将check[4]赋值为0,base[4]赋值为1.
-
输入a, 发生冲突
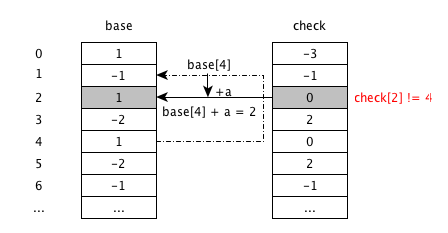
根据base[4]+4 状态从4跳转到2, 但是check[2]非空,并且check[2]=0不等于父状态4,此时发生冲突
-
解决冲突
-
挪动以4为父状态状态转移,查找对应base,check的连续的空闲空间以放入状态。这里只有最新的输入a带来的状态转移以4为父状态。base[6], check[6]有空闲。
-
修改base[4], 使其能够根据输入跳转到空闲空间,即base[4] = 6 - a = 5.
-
重新插入a. 如下图
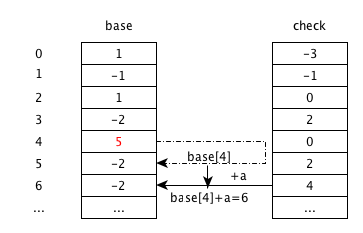
-
-
已有的实现代码
由于业务中需要用到java,找到了一个已有java代码实现地址:https://github.com/digitalstain/DoubleArrayTrie, 但存在一些问题
- 问题
- 代码本身的问题
- 该代码接口不易使用,均是对int数组的操作,需要对字符串映射后使用
- 代码应用场景与我们的业务不同,应用于根据对大量单词建立trie树,然后输入一个串判断是否是某个单词的前缀,与我们的匹配方向刚好相反
- 算法实现的问题
- 目前在处理叶节点时,均是用一个特殊的数字标识-2,但是上述例子接着插入abc这样的前缀时,由于b在前缀ab中已经标识为-2叶节点,此时check检查也是相同的父节点,如果覆盖了base中的值,b为叶节点的信息就会丢失。
- 解决方案:为前缀结尾增加一个特殊字符‘\0’用来标识结尾,插入方法不变。查找时,需要每个父节点除了接收字符跳转意外,还需要加特殊字符跳转到某个状态,检查base值是否-2为叶节点,以匹配前缀到此结束的情况。
- 代码本身的问题
对算法进行Tail优化
根据论文An Efficient Implementation of Trie Structures, 针对上述DATrie算法还能一个tail的改进,即每个前缀的最后的结尾单独存储在一个数组里,由base里存储的值指向该tail。
例如, a 和 abcd作为前缀输入后,bcd作为一个单独的tail另外存放到一个字符串数组里。
-
速度 减少了base, check的状态数,以及冲突的概率,提高了插入的速度。在本地做了一个简单测试,随机插入长度1-100的随机串10w条,no tail的算法需120秒,而tail的算法只需19秒。 查询速度没有太大差别。
-
内存 状态数的减少的开销大于存储tail的开销,节省了内存。对于10w条线上URL,匹配12456条前缀,内存消耗9M,而no tail的大约16M
-
删除 能很方便的实现删除,只需将tail删除即可。
基于上述,重新实现了一个java版的前缀匹配在团队内使用。